RNN(循环神经网络)简要介绍

简介

循环神经网络模型以序列数据为输入（数据内部的元素是有顺序关系的），如文章、语句、一周的天气信息、三个月的股市指数等。与传统的前馈网络不同的是，RNN模型处理序列数据能够获取更多的语义信息，时序信息等。

处理任务示例：

以NER（命名实体识别）为例，从自然语言文本中识别真实世界中的实体名及其类别。如：

句子1：I like eating apple!——其中的apple指的是苹果食物

句子2：The Apple is a great company！——其中的Apple指的是苹果公司

而如果是传统的DNN（深度神经网络）模型，由于输入方式为逐元素输入，无法有效获取上下文信息，则若训练集中的apple一词大部分被标记为苹果食物，那么对测试集中的apple处理也将全部标记为苹果食物而非根据实际上下文推断。

模型提出

基本RNN结构

为了解决普通DNN（深度神经网络）逐元素输入而无法有效获取上下文信息的问题。RNN最基本的改良点在于增加一个模块用于储存上下文信息，下图即是一个典型的RNN结构示意：

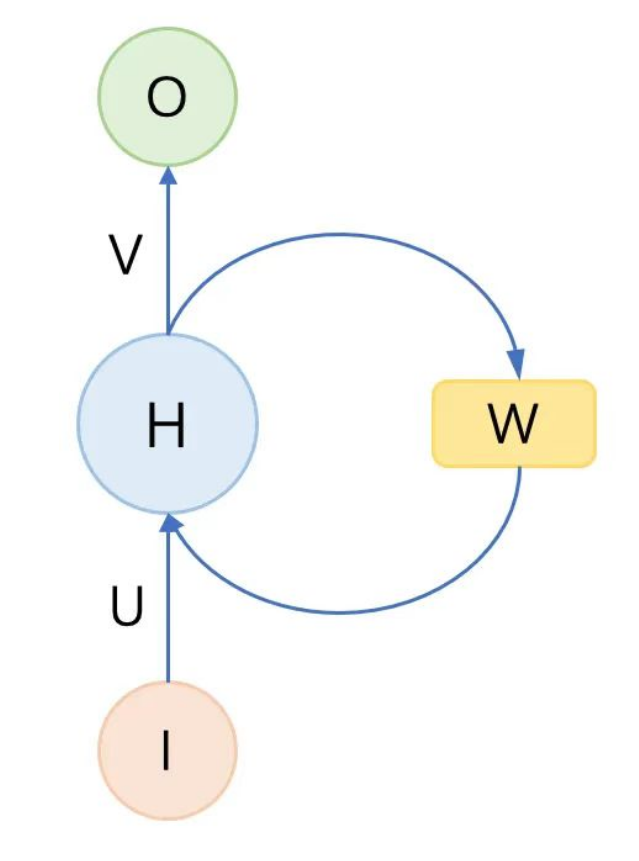
image-20250417165208064

其中I（输入序列）到O（输出序列）的过程增加了一个保存上下文信息的权重矩阵W，也就是每次输出O不仅要考虑当前的输入数据I，还要考虑上一次输出的隐藏序列W（保存上下文）。RNN就是一个循环递归地处理上述输入输出的过程。

RNN展开结构

将上图的基本结构展开，就成为了下图展示的模型计算过程：

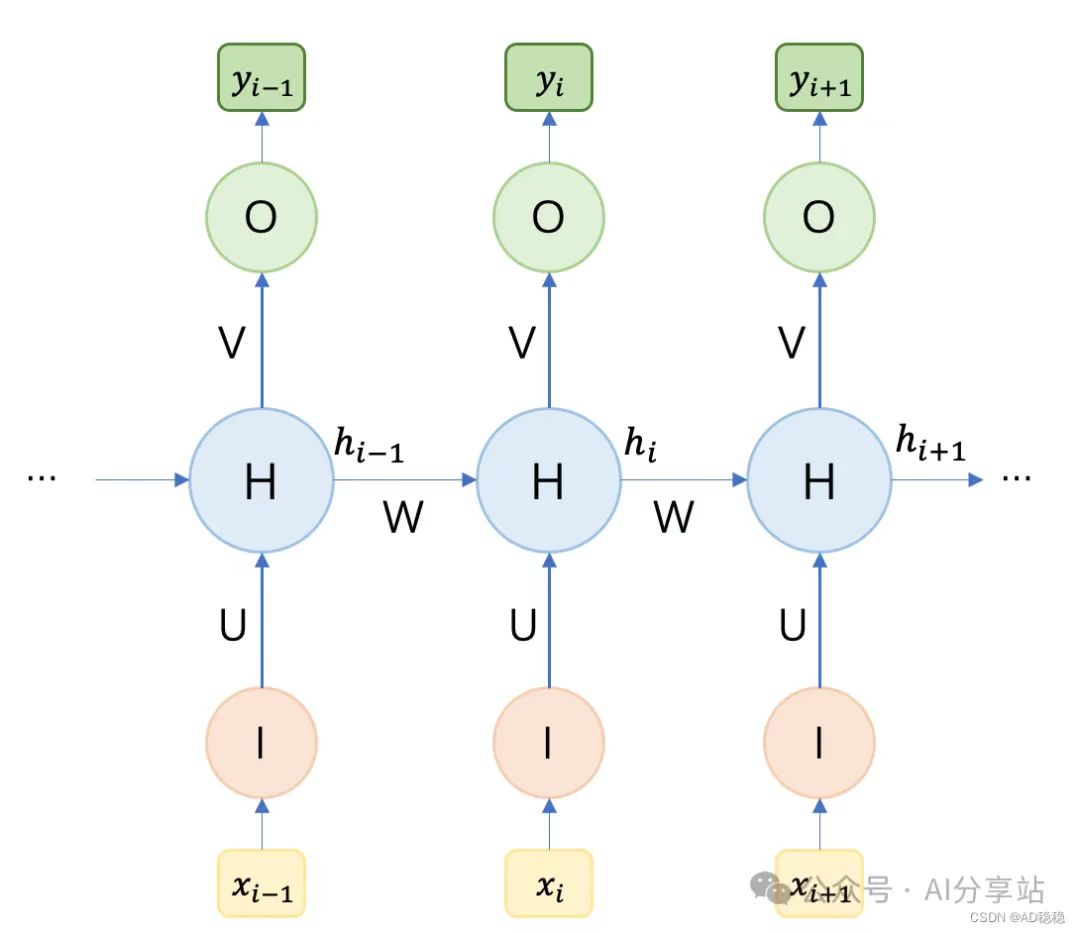
ebe46967a3e80dab4c04635a2c6785f

其中 \(x_i\) 表示i时刻的模型输入，\(y_i\)表示\(x_i\)对应的输出结果，模型计算公式如下： \[ \begin{split} y_i = g(Vh_i) \\ \\ h_i = f(Ux_i + Wh_{i-1}) \end{split} \] U表示当前输入数据的权重因子，W表示决定上下文信息影响程度的参数矩阵，\(h_i\)则表示当前隐藏层的输出隐变量。可以看出决定当前输出\(y_i\)的隐变量\(h_i\)不仅由当前输入\(x_i\)决定，也与上一时刻的隐变量\(h_{i-1}\)有关。（PS：整个模型计算过程里用的参数矩阵W是一定的）

RNN模型结构变化

上述展开结构会根据输入长度和输出长度的变化而产生不同的结构

N to N结构

这类结构的输入长度与输出长度相同，也即每一个输入值都会对应一个输出值。通常用于逐序列判断或分类任务（如序列标注，NER，视频帧分类等）。示例图与计算模型如2.2所述。

N to 1结构

这类结构只有一个输出值，表示输出结果包含了整个输入序列的语义信息和上下文信息。结构示意图：

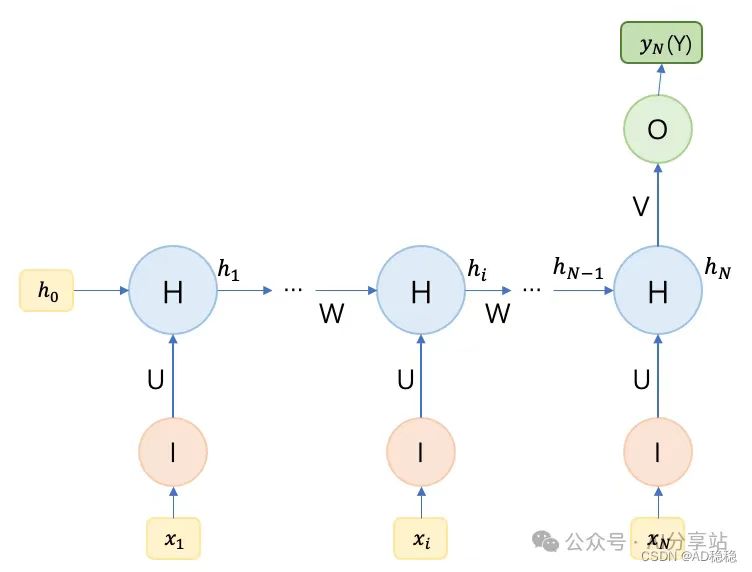
8606007dd425e9195f0c11d4719656f

计算模型： \[ \begin{split} Y = y_N = g(Vh_N) \\ h_i = f(Ux_i+ Wh_{i-1}) \end{split} \] 这类结构通常用于文字分类、文章分类以及图像分类任务。

1 to N结构

一个输入数据对应一系列输出，其意义是一个起始状态或种子数据会随时间变化生成一个序列的输出结果。

若输入数据只在首个时刻输入，则计算示意图如下所示：

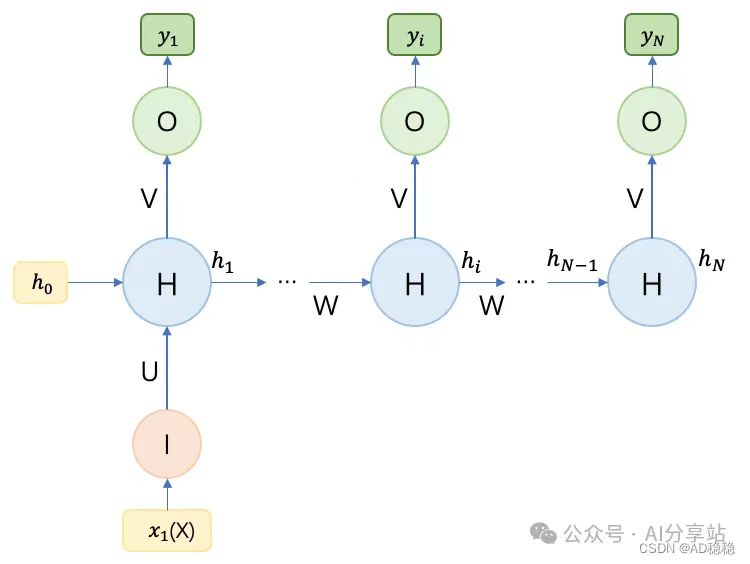
112ce7e4cbc3de28915ec314a82fdba

而若输入数据在每个时刻都作为输入，则示意图如下：

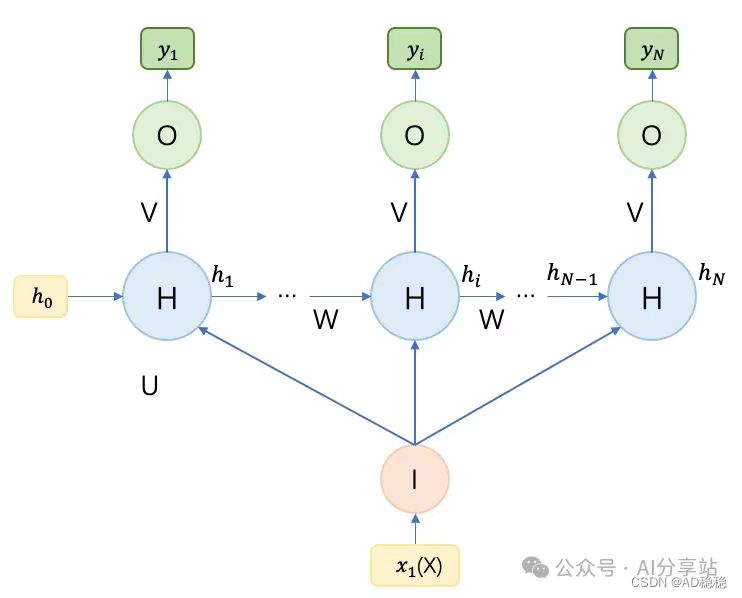
bd9767d63cc2fd88b9b265d80777250

该结构通常用于由图像自动生成文章、类别生成音乐、文章、代码等由种子数据生成序列的任务。

N to M结构（encoder-decoder模型、seq2seq模型）

最后一类是输入输出序列长度不相等的结构。通常采用一个N to 1结构和一个1 to M结构组合来实现，如下图：

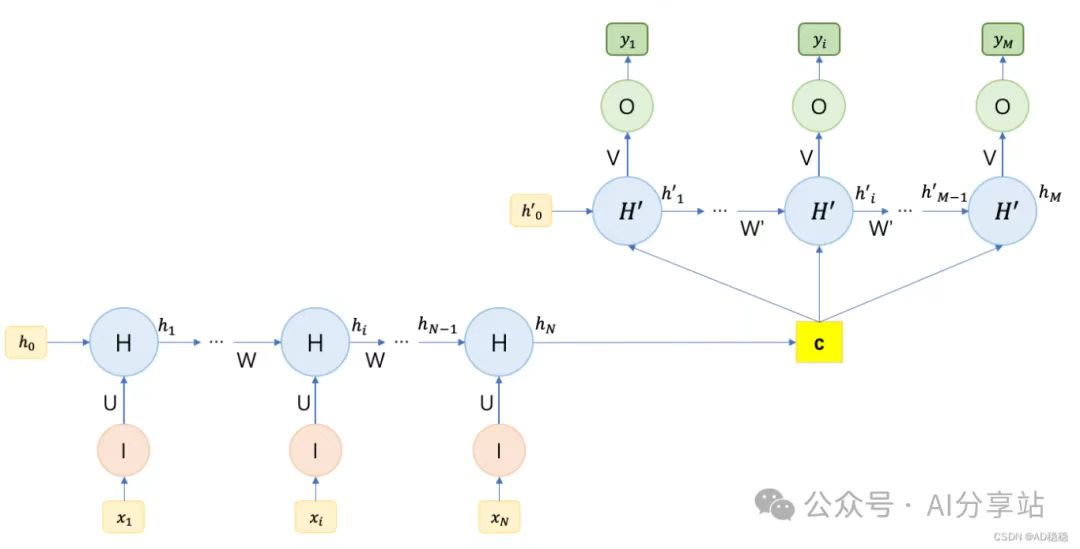
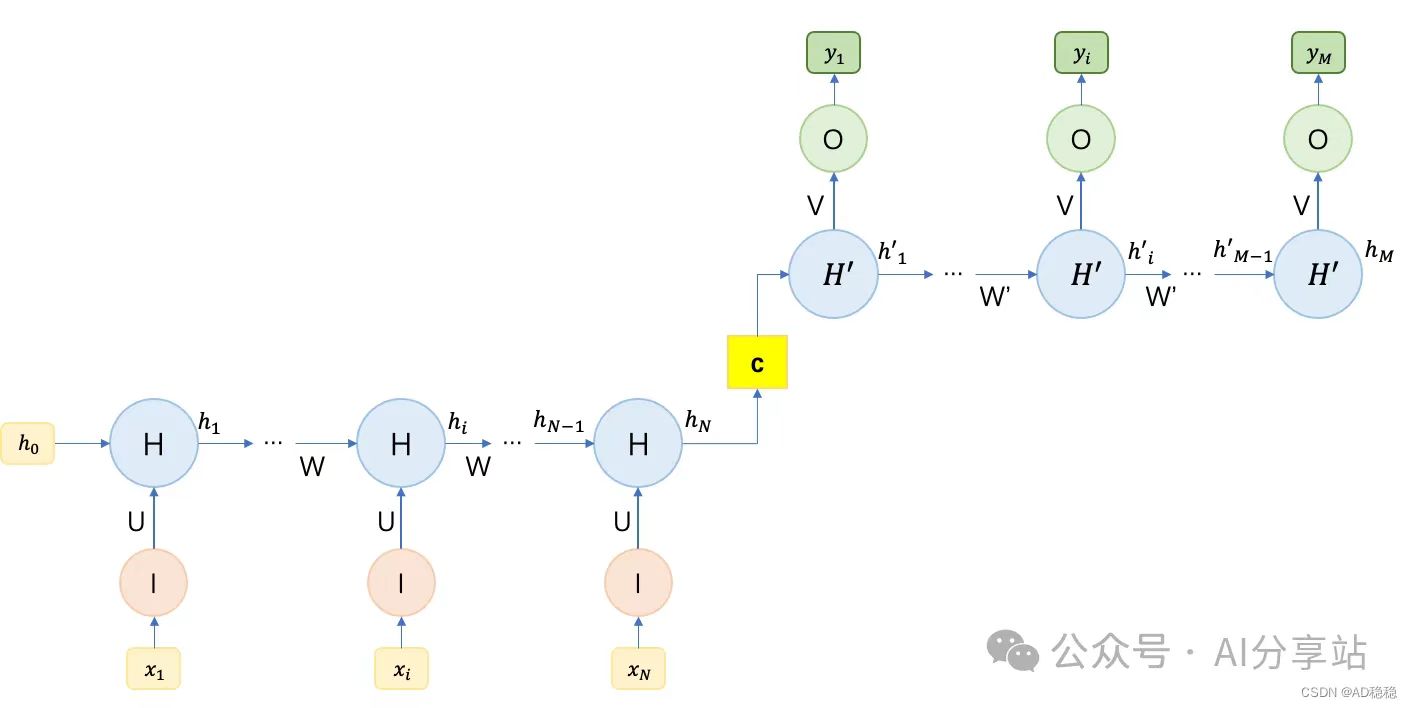
f529bf34ed1f0a34e98af6cd3b390b2 6355d703227ac85b3ac67a61c52bd84

由上图可以看出，两个不同长度的RNN模型组合可以控制输出序列长度。两个模型之间通过一个上下文向量C来链接，其中C可作为第二个RNN模型的输入数据并对初始隐藏变量\(h_0^{'}\)​进行初始化（如第一个图），也可以直接被用来初始化第二个RNN模型的隐藏变量（如第二个图）。

常用的上下文向量C的求解方法有： \[ \begin{split} c = h_N \\ c = g(h_N) \\ c = g(h_1 :: h_N) \end{split} \] 第一种方法直接将encoder的输出作为上下文向量；第二种方法则需要先对encoder输出进行变换；第三种方法则将encoder的一个输出序列进行变换，而非单一选取最后一个输出。

通常将第一个RNN模型作为encoder（编码器），第二个RNN模型成为decoder（解码器）。通过这样N to M的RNN模型，我们可以处理各类序列处理任务，如语音识别，文本摘要，机器翻译，图像描述生成等。

梯度消失与梯度爆炸

概念

由于RNN中的上下文参数矩阵是权重共享的，即当进行梯度更新时，对该矩阵求偏导数时需要加入时序影响，将导致存在基于时序数量的权重“连乘”。若某一阶段权重值过小，结合“连乘”将导致最终权重趋于“无穷小”（即等于0），此现象称为“梯度消失”。相反地，若权重值过大，经连乘后将导致权重值变得过大，称为“梯度爆炸”。

与普通NN的梯度消失及梯度爆炸不同，RNN的梯度爆炸（或消失）是根本原因是“连乘”，是在反向传播的某一阶段出现的，在此之前的反向传播不受影响。

如何解决

1. 梯度爆炸的解决

1）梯度裁剪

​ 梯度裁剪即为梯度更新时的梯度设置上限，当超过阈值将强制裁剪，避免出现过高阈值。

2. 梯度消失的解决

1）使用Relu激活函数

​ 使用Relu激活函数解决梯度消失的原理是，Relu函数在自变量大于0是，因变量恒为1，由此避免梯度过小。

2）变更RNN结构

​ 改用变种版本的RNN结构，常见的包括LSTM模型及GRU模型。